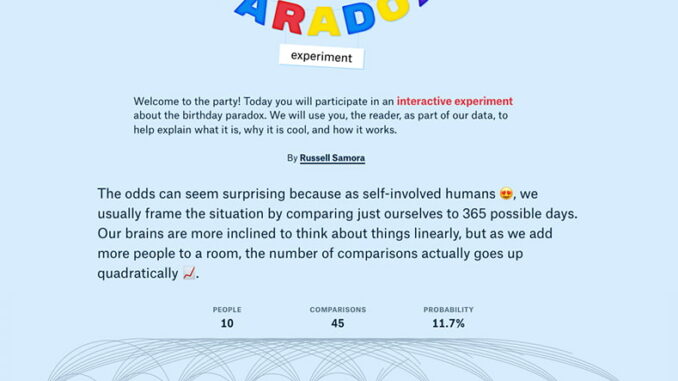
Este es uno de los problemas matemáticos más famosos sobre probabilidad, tan contrario a la intuición humana que lo clasificaron como paradoja: el problema/paradoja del cumpleaños:
Para presentar la archiconocida paradoja del cumpleaños se suele hacer ver a los asistentes a una clase cuántas personas hay –quizá 30 ó 40– y que un año tiene 365 días. Luego se pregunta si creen probable que dos personas cumplan años el mismo día (la respuesta suele ser que no). También se puede pedir estimar cuántas personas harían falta para que la probabilidad de que esto suceda sea más del 50% (normalmente se escucha que cientos).
La realidad es bien distinta. Pero como las matemáticas a veces son difíciles de digerir, Russell Samora diseñó una perfecta explicación con muñequitos animados en la que paso a paso se puede entender lo que sucede. Se puede disfrutar en El experimento sobre la paradoja del cumpleaños.
La página de ThePudding no recopila datos personales, aunque te pide tu fecha de nacimiento para hacer la demostración y luego va guiándote por unas y otras opciones según vayas contestando. A partir de cierto momento, para simular la ley de los grandes números, pasa al modo supervelocidad e hipervelocidad. Sencilla y directa, paso a paso, como son todas las buenas explicaciones.
Me pareció una iniciativa estupenda, que aunque está en inglés puede servir a los más jóvenes y a los menos avezados en probabilidad para introducirse en el problema y, por ende, en el fantástico mundo de las paradojas. Aunque parezca una paradoja ejemplificada de una forma muy peculiar, lo cierto es que sus bases aparecen continuamente en el MundoReal™ y conocer sus fundamentos es algo que siempre viene bien.
Relacionado:
El problema/paradoja del cumpleaños
Un simulador de la «paradoja del cumpleaños» nos enseña que los humanos no somos muy buenos estimando probabilidades
Diez hechos matemáticos sorprendentes

Dejar una contestacion